“Tell me and I forget, teach me and I remember, involve me and I learn.”
- attributed to Benjamin Franklin
An estimated 50 percent of adults suffer from math anxiety and research indicates that discomfort with numbers can begin as early as first grade. Students who have not experienced success in traditional educational settings exhibit math anxiety frequently — creating a regular challenge at Rock Point School. Let's explore the hands-on approach used by our math department to build confidence by doing.
Hands-On Learning
A student's educational experience in math and science can build confidence and be enriched and reinforced through interactive, hands-on learning, also known as kinesthetic learning. The benefits have been much studied and reported on: most notably - greater stimulation for learning, greater possibilities for retention, and increased critical thinking skills. It can also allow for integrating analytical, construction, and visualization skills in one learning experience.
Jean Piaget a renowned psychologist who studied how humans get, keep, and develop knowledge was a strong advocate for hands-on learning in the classroom. The famed Montessori method (PDF) of education is centered around hands-on learning experiences.
Learning Math
At Rock Point, we like to incorporate such practices in classes whenever possible, especially in math and science. Such approaches work especially well in the small classes we have here. Doing math is sometimes thought of as primarily a ‘pencil and paper’ endeavor but understanding mathematical concepts can be enhanced through hands-on activities such as geometry constructions using a compass and ruler, building and using devices to draw plane curves, or simple examples of motion studied in physics.
Three Examples in Practice
Here are three examples we worked on with students in math that give a sense of what can be accomplished with very simple physical setups, measurements, data analysis, and computer software to illuminate related mathematical and scientific concepts.
It is important to note that the materials used in hands-on activities don’t have to be expensive or complicated; ‘canned’ educational products are certainly not required. In fact, using simple materials and home-made devices often provides an opportunity for students to be involved in helping to improvise their own learning experience as it happens. There are also a number of free online or downloadable software packages that are useful for a variety of mathematical analyses.
The Simple Pendulum
The first hands-on experience involves one of the most famous examples of circular motion in physics: the pendulum. (A pendulum is a weight suspended by a string or rod from a fixed support; the string or rod plus weight swings back and forth.) A child's swing and a wrecking ball are everyday examples of pendulums. In the history of technology, the pendulum is most notable for its use in clocks for accurate time keeping but also in seismographs for sensing earthquake activity.
We had the students study the motion of a pendulum, working in teams of three. Their pendulums were made from a threaded nut as the weight supported by a string hanging from a fixed support. They released the nut from rest at and recorded the swinging motion using smart phone video. Then they took measurements of the angle of the string as a function of time using motion tracking software (Tracker 1.5). See Figure 1 for a photo of the pendulum and a screenshot from Tracker 1.5. The software permits measurement of the angle frame-by-frame using a built-in virtual 'protractor'! They recorded the angle and time for each video frame for one full swing and entered that data into a Google spreadsheet. Using the spreadsheet, they plotted the angle versus time.
Figure 1: The pendulum set up and a screenshot of Tracker 1.5 software with a student video embedded for measuring the angle of the pendulum string. Tracker 1.5 enables measuring location and orientation data versus time by stepping through a video file frame-by-frame.
Lo and behold, the plot looks like a cosine function! That's what the data shows. What about the theory of pendulum motion, as predicted by the laws of physics? Do the measurements agree with the motion predicted by a model subjected to Newton's Laws of Mechanics? It turns out that the angle of the pendulum released from rest predicted by solving the equations of motion is a cosine function. So, the data from measurements corroborated the theory. Cool
Special Planar Curves: the Cycloid
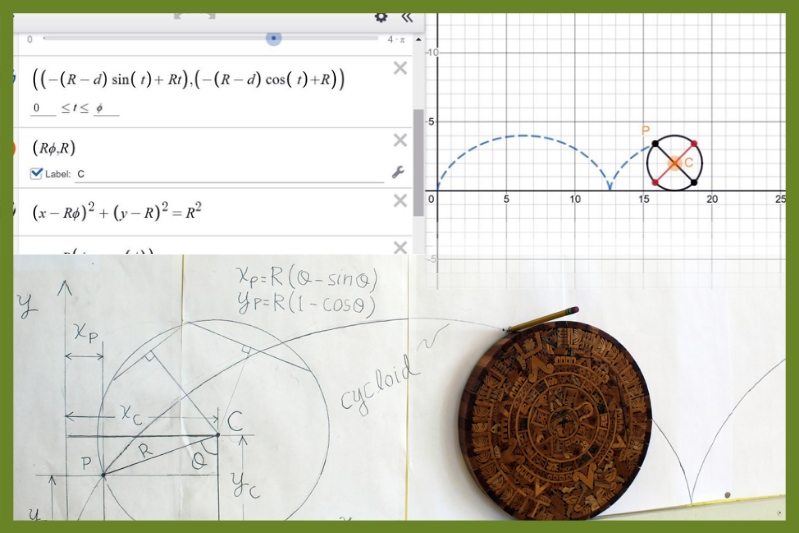
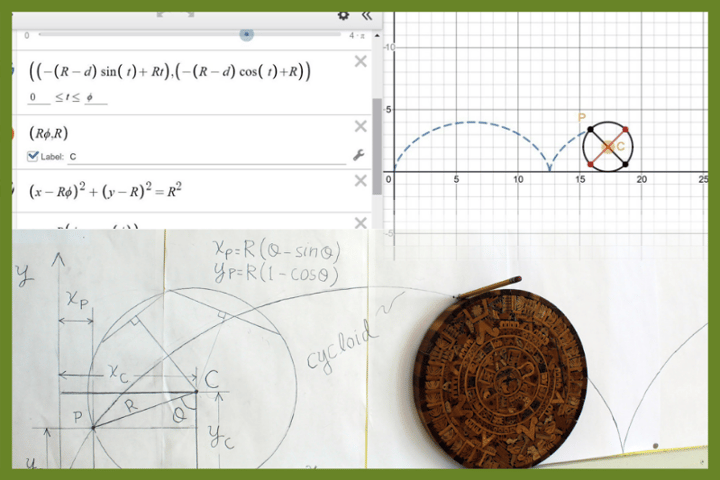
The second example involves the study of a special planar curve: the cycloid (a path of a point on the rim of a wheel rolling without slip). The project involved building physical demonstrations, deriving the equations of the path using the geometry of constrained motion, and computer simulation and animation using Desmos, an online graphing software package. See Figure 2 for a picture of the construction.
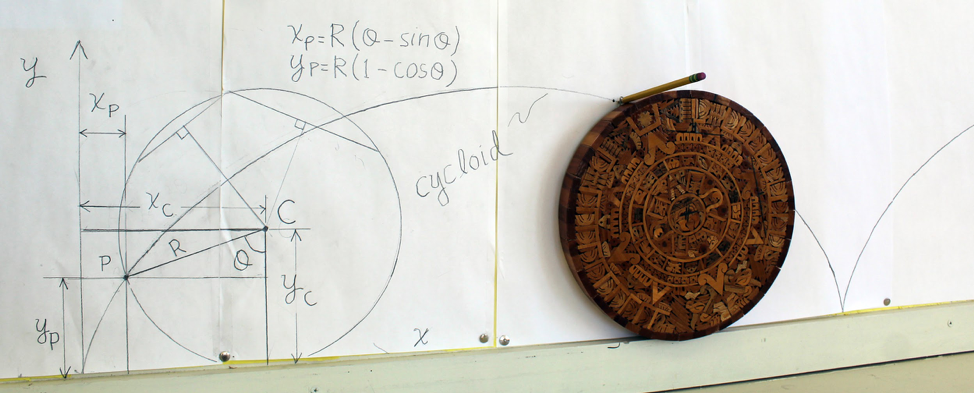Figure 2: Student construction of a cycloid curve using materials at hand in the classroom. The student rolled the wooden disk so it didn’t slip on the ledge (with a pencil attached to the outside) to trace out the path. She then drew in the different quantities of interest used in deriving the parametric equations for the x and y coordinates of a point P on the cycloid, in terms of the radius of the disk (R) and the angle of rolling (𝜃).
Although the main purpose of the exercise was to construct a cycloid, an unexpected hands-on learning opportunity arose: locating the center ‘C’ of the circle using perpendicular bisectors of two chords of the circle - created using only a compass and straightedge! See a still image in Figure 3 of the simulation and animation that the student created using Desmos. (Here is a link to the Desmos file created by the instructor.) Note that the cycloid generated from the mathematical equations that describe as depicted with the software mimics quite well the path generated physically as shown in Figure 2 - a pleasing result for a student.
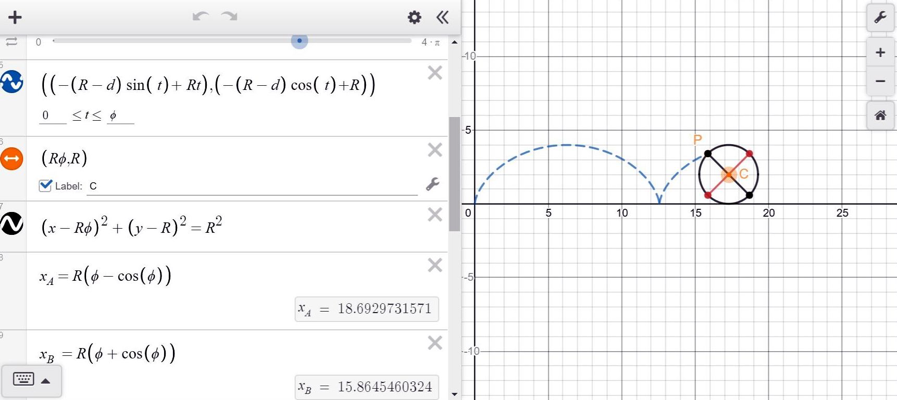Figure 3: Still image of the simulation and animation of a cycloid created by a point P on the edge of a disk of radius R rolling without slip from a Desmos file. The student entered the cycloid equations into Desmos for the path of point P, but also had to add additional equations and features to make a ‘cartoon’ of the rolling disk. This ‘hands-on’ computing aspect of the exercise required the student to use spatial skills in a sophisticated way that gave some insight into what is required in developing various tools for animation in various media such as gaming or cinema.
Drawing Ellipses
The last example involves drawing ellipses using two approaches: the ‘string-and-pins’ method and a trammel ellipsograph (or trammel of Archimedes). The ellipse is a special plane curve, one of the conic sections. In the first case, given a fixed length of string and two pins separated by a known distance, the students could draw an ellipse and show how those two quantities are related to the standard equation of an ellipse centered at the origin of a coordinate system. Likewise, the students could use a trammel ellipsograph made from Lego to draw an ellipse and then relate the parameters that describe the device to the standard ellipse equation (see Figure 4).
Figure 4. A trammel ellipsograph also known as the Trammel of Archimedes is a device that can draw ellipses (shown on the left). This one is constructed from Lego’s. A ‘string-and-pins’ construction for drawing an ellipse is shown on the right.
Summary
A hands-on learning approach offers a special opportunity for an effective way to overcome math and science anxiety. Focusing on specific physical tasks is fun, demonstrates math and science principles — and can alleviate a negative learned response to math.
Resources
Our Students Have Math Anxiety — Now What?
Timed Tests and the Development of Math Anxiety
------------------
Authors: Hans Manske and Michael Coleman